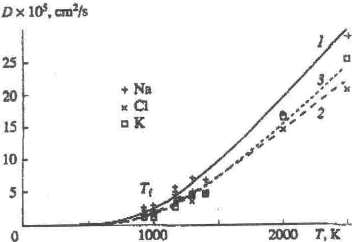
Fig. 1 .
Inorganic Materials, Vol. 30.
No. 4, 1994. pp., 483 - 485. Translated from Neorganicheskie Materialy, Vol. 30, No., 4. 1994, pp. 514 - 516. Original Russian Text Copyright @ Why Znamenskii, Savintsev, VI Zil'berman, Savintsev.Parameters of Contact Melting in Ionic Systems: Molecular Dynamics Simulations with Pauling and Fumi-Tosi Potentials
V.S. Znamenskii*, P. A. Savintsev*, P. F. Zil'berman**, and A. P. Savintsev*
Received September 28,1993
INTRODUCTION
Contact melting is widely used both in various engineering processes and in physicochemical analysis [1-5] . It is successively used to produce permanent joints, construction materials, alloys, and chemical compounds. Contact melting serves in constructing fusibility diagrams and in simplifying investigations of diffusion processes. In particular, it allows one to easily determine interdiffusion coefficients and partial diffusion coefficients [6] . However, studies of contact melting involve technical difficulties and are not always possible for a number of systems. Therefore, methods of computer simulation have come into use recently for studying this effect: the molecular dynamics method is the most promising among them [7] ,
One of the main parameters of contact fusion is its temperature Tf . Ordinarily, it is determined theoretically by analyzing the fusibility diagrams of systems. In order to correctly determine Tf by molecular dynamics simulations, it is necessary to choose a proper pair potential. The Pauling and Fumi-Tosi potentials are used for ionic systems. In this work, we compared the simulation results on contact melting in the NaCI - KCl system for both of the potentials [8] .
RESULTS AND DISCUSSION
In the simulations we used the following model.
(1) The initial location of Na, Cl, and K particles in the simulation box is represented by a cubic lattice with oppositely charged nearest-neighbor ions; Na+ and K+ ions occupy opposite halves of the box so as to imitate the contact between NaCI and KCl.
(2) The simulation box is a cube of constant edge length.
(3) Periodic boundary conditions are used.
(4) During a given simulation, a constant-temperature condition is maintained by multiplying velocities by a scaling coefficient.
(5) The forces of pair Interactions arc calculated preliminarily, and tables of fi /r are used n simulations. Here f is the force; r is the distance between the particles; and i = 1, 2, ... , 6 is the number of the type of an interacting ion pair. Our simulations involved a total of six types of pairs, namely, Na-Na, Na-Cl, Cl-Cl, Na-K, Cl-K. and K- K.
We used the following numerical parameters.
(1) The ionic weights (kg) were: 38.2 x 10-27 for Na, 58.9 x 10-27 for Cl. and 64.7 x l0-27 for K.
(2) The numbers of Na, Cl, and K ions in the simulation box were 54, 108, and 54, respectively.
(3) The edge length of the box is 2.35 X 10-9 m; this corresponds to 1.3 times the edge of the cube whose volume is equal to the volume occupied by the ions at 0 K.
We calculated the box volume using the Pauling pair potential. The time-integration step used was 6.26 X 10-15 s. In order to obtain the time dependence of mean-square displacement of particles from their initial positions and to calculate diffusion coefficients from this dependence, we fixed current coordinates of the particles every 32 steps. We determined diffusion coefficients using a linear fit of the mean-square displacements calculated at 32 instants in time for Na+ ions, Cl- ions that were initially located in the half of the simulation box containing Na+ ions, K- ions, and Cl- ions initially located in the half of the simulation box containing K+ ions. Thus, we determined the diffusion coefficients by analyzing the system for about 13 x 10-12 s from the onset of contact.
Table 1. Parameters of the Fumu-Tosi potential
|
Type of interacting Ions |
C x l025, J nm6 |
d x 1027, J nm8 |
b ij |
a ij, nm-1 |
|
Na-Na |
1.7 |
0.8 |
1.25 |
31.55 |
|
Na-Cl |
11.2 |
13.9 |
1.00 |
31.55 |
|
Cl-Cl |
120.2 |
241.7 |
0.75 |
30.61 |
|
Na-K |
13.0 |
12.4 |
1.25 |
30.61 |
|
Cl-K |
48.0 |
73.0 |
1.00 |
29.67 |
|
K-K |
24.3 |
24.3 |
1.25 |
29.67 |
Self-diffusion coefficients of (1) Na+, (2) Cl-, and (3) K+ ions in the system modeling the NaCl-KCI contact. The coefficients were calculated in molecular dynamics simulations using the Pauling pair potential at various temperatures for a constant volume.
The Pauling and Fumi-Tosi potentials were used in the simulations.
The Pauling potential Vij for the ions under consideration had the following form [7] ;
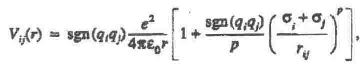
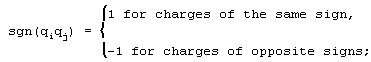
p = 8 specifies the rigidity of the repulsive term of the potential; and e is the elementary charge.
Table 2. Diffusion parameters of ionic system
| System | Method | Ion | A x 103, cm2/s | E x l0-3, J/mol |
| NaCl |
Experiment
[11] |
Na
Cl |
3.36
3.02 |
33.0
35.2 |
| NaCl-KCl | Calculation using the Pauling potential |
Na
Cl K |
1.6 ±0.30
121 ±0.18 153±0.14 |
35.3 ±1.7
35.7 ±1.7 38.6 ±0.8 |
| NaCl-KCl | Calculation using the Fumi-Tosi potential |
Na
Cl K |
1.7 ±0.2
1.9 ±0.3 1.8 ±0.2 |
37.4 ±13
41.6 ±1.7 37.8 ± 13 |
Self-diffusion coefficients of (1) Na+, (2) Cl- initially located in the Na-containing half of the simulation box, (3) K+, and (4) Cl- ions initially located in the K-containing half of the simulation box; the coefficients for the system modeling the NaCl-KCl contact were calculated molecular dynamics simulations using the Fumi-Tosi pair potential at various temperatures for a constant volume.
The Fumi-Tosi potential was used in the form [9]
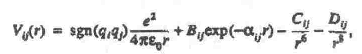
where Bij = b ij bexp[ a ij( s i+ s j)]; a ij and b ij are the tabulated parameters, and 6 = 3.38 x 10-20 J.
In this case, s 1 = 11.7 x 10-2 nm, s 2 = 15.8 x 10-2 nm, and s 3= 14.6 x 10-2 nm.
Table 1 lists the van der Waals coefficients C and D, as well as a ij and b ij.
We carried out numerical simulations at various temperatures; the temperature dependencies of the diffusion coefficients are presented in Figs. 1 and 2 . Figure 1 shows the data obtained using the Pauling potential, whereas Fig. 2 shows that for the Fumi-Tosi potential. It is seen that the temperature dependences follow an exponential law
D=Aexp(-E/RT)
for both of the potentials.
The diffusion coefficients obtained are of the same order of magnitude as those reported for ionic melts. A comparison of the calculated parameters with the results obtained with radioactive tracers and contact melting [10] shows mat the calculated activation energies E are closer to the experimental values in the case of the Pauling potential. As for the preexponential factors A, they are closer to the experimental values if calculated using the Fumi-Tosi potential (Table 2) .
The ratios of the diffusion coefficients for Na, K, and Cl calculated with the Pauling potential are closer to the experimental ratio than those calculated using the Fumi-Tosi potential. It should be noted, however, that the error in the diffusion coefficients calculated with both potentials was about 10%, whereas the experimental error was ordinarily greater (15 - 20%).
Contact melting is known to be a phase transition of the first order and to have some specific features. We used these features in estimating Tf by molecular dynamics simulation. For example, an abrupt change, to the diffusion coefficient should occur at the transition temperature. We can account for this behavior as follows. Neglecting solid-state diffusion and significant fluctuations of the diffusion coefficients, we can assume that diffusion caused by the formation of a liquid phase at the contact interface develops at the contact-melting temperature Tf and notably increases at higher temperatures. A comparison of the contact-melting temperatures calculated in the molecular dynamics simulations with different potentials showed that the temperature obtained with the Pauling potential [(936 ± 8) K] is in better agreement with the experimental value (932 K).
CONCLUSION
Melting at the NaCl-KCl contact was analyzed by molecular dynamics simulations. Macroscopic melting parameters can be calculated using both the Pauling and Fumi-Tosi potentials. The use of the Pauling potential results in better agreement with the experimental data.
REFERENCES
1. Savintsev, P.A., and Avericheva, V.E., On the Melting Point of a Crystal Contact Layer, Dokl. Akad. Nauk SSSR, 1958, vol. 119. no. 5. pp. 936 - 937.
2. Zilberman, P.F., and Savintsev, P.A., Contact Melting of Alkali Sulfates, Nitrates, and Nitrites, Izv. Akad. Nauk SSSR, Neorg. Mater., 1989, vol. 25, no 2, pp 318 - 321. 321.
3. Zil'berman, P.F., and Savintsev, P.A., Contact Melting in the KNO3-Na2CO3 System, Zn. Fiz. Khim., 1992, vol. 66. no. 2, pp. 521 - 525.
4. Zil'berman, P.F., and Savintsev, P.A., Contact Melting in Crystals of Alkali Halides, Neorg. Mater., 1992, vol. 28, no. 3, pp. 614-618.
5. Znamenskii, V.S., Savintsev. P.A., and Zil'berman, P.F., Molecular Dynamics Study of the Contact Melting-Method. Russ. J. Phys. Chem., 1993. vol. 67. no. 7, pp. 1349.1352.
6. Zilberman, P. and Savintsev, P., The Contact Melting as the Method of Investigation of Diffusion Process in Melting Salts, Third Int. Symp. on Molten Salt Chemistry and Technology, Paris, 1991.
7. Hockney, R.W., and Eastwood. J.W., Computer Simulation Using Particles, New York: McGiaw-Hill, 1981.
8. Savinisev, P.A., Zil'berman, P.F., and Znamenskii, V.S., The Use of Personal Computers m Molecular Dynamics Siinuliaiuns of Contact Melting in Ionic Crystals, Nauchnye Soobshcheniya VII Vsesoyuznoi Konferentsii po Stroeniyu i Svoistvam metallicheskikh i Shiakovykh Rasplavov (Proc. VII All-Union Conf. on the Structure and Properties of Metal and Slag Melts), Chelyabinsk: Chelyabinsk Politeknn. lnst, 1990, vol. 1. part 2. pp. 207-208.
9. Sangster, M.J.L., and Dixon, M., Interionic Potentials in Alkali Halides and Their Use in Simulation of Molten Salts. Adv. Phys., 1976, vol. 25, no. 3. pp. 247 - 342.
10. Zil'berman, P.F., Contact Melting of lonic Crystals. Cand. Doctorate (Phys.-Mat.) Dissertation, Tomsk,1993.
11. Bloom. H., and Bockris. J.O.M., The Structure of Ionic Liquids, Fused Salts, Sundheim, B.R.. Ed., New York: McGraw-Hill, l964.