Platonic Solids and High Genus Covers of Lattice Surfaces

Jayadev S. Athreya, David Aulicino, and W. Patrick Hooper, with an appendix by Anja Randecker

Trajectories on the Dodecahedron

Press the button to start the animation.

Start!

Press the button to stop the animation.

Stop!

From Appendix C of the second paper: Showing a representative closed saddle connection from coset number (please wait).
Change saddle connections:
Decrement (-) Increment (+)

Student Activities: Make your own dodecahedra! Click the figure or link below for instructions.

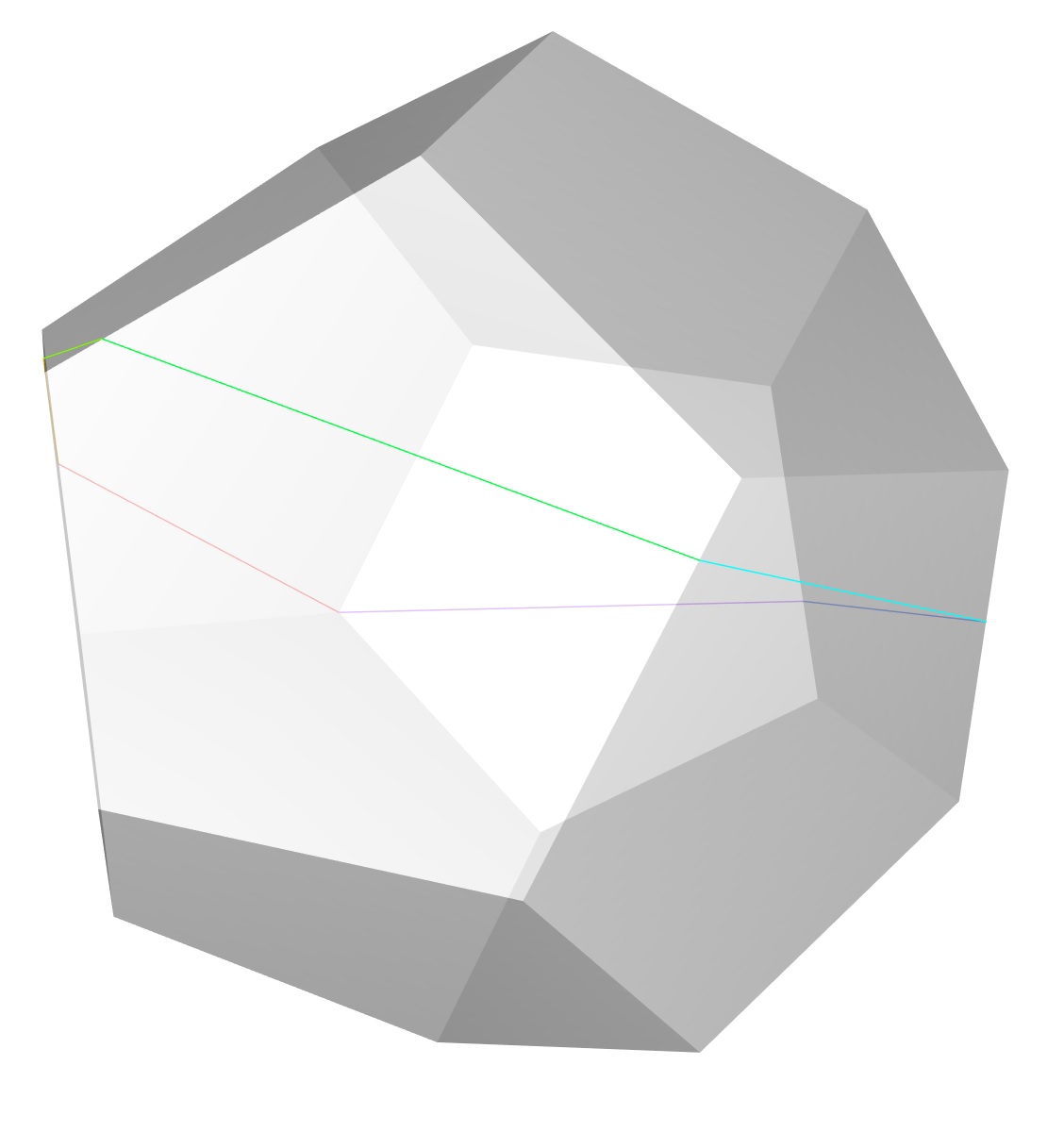
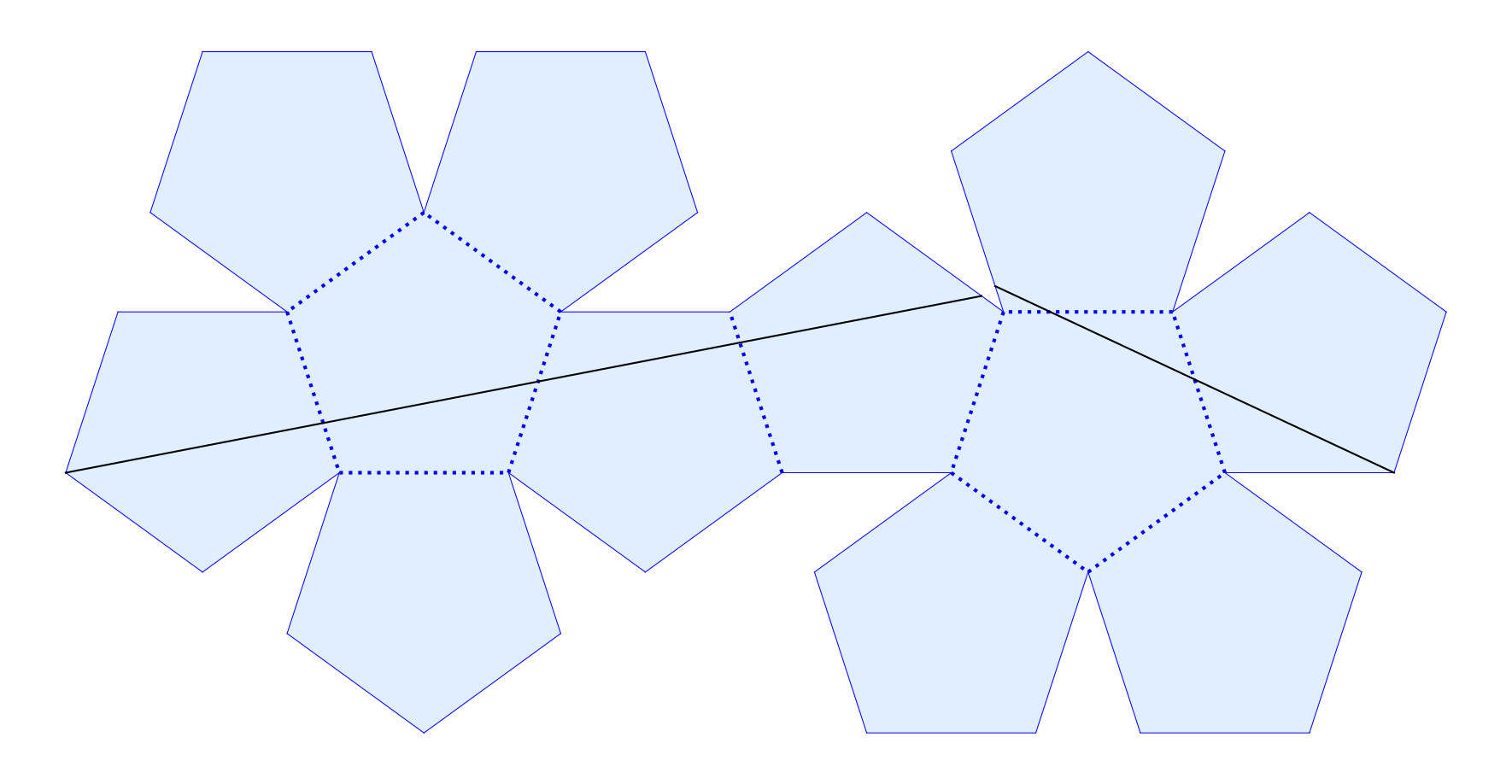
Click the figure below to download the complete pdf of representatives for all closed saddle connections. The pdf contains nets of the dodecahedron such that each net contains a representative closed saddle connection corresponding to the coset listed by its number in Appendix C of the second paper. These can be printed on paper, cut out, and taped together to get the models of the dodecahedra in the animation above.

Dissemination

1. MFO Snapshots
2. Numberphile
3. Quanta Magazine
4. Vice
5. N+1 (русский)
6. Forskning & Framsteg (svenska)

Papers

1. J. S. Athreya and D. Aulicino, A Trajectory from a Vertex to Itself on the Dodecahedron. arXiv:1802.00811, The American Mathematical Monthly, 126:2, 161-162 (2019).
2. J. S. Athreya, D. Aulicino, and W. P. Hooper, with an appendix by Anja Randecker, Platonic Solids and High Genus Covers of Lattice Surfaces. arXiv:1811.04131, (Accepted. To appear in Experimental Math.). Preprint: 1-51 (2018).

Talks

• Talk of D. Aulicino at Graduate school on Geometry of Teichmuller spaces April 15-19, 2019 at the Simons Center

Sage Notebooks and Auxiliary Files

Download all of the files below in a single zip file (Updated: May 1, 2020)

1. code_from_the_article.ipynb, (html Version): This goes through all of the primary code occuring in the main text of the second paper. (Updated: May 1, 2020)
2. Figures.ipynb, (html Version): This contains all of the code necessary to generate the figures from the second paper. (Updated: May 1, 2020)
3. wordlist: This contains all of the coset representatives reduced under the unfolding-symmetry relation needed in Section 9.5 of the second paper. (Updated: December 19, 2019)
4. r, t: These are the monodromy permutations in S₂₁₀₆ for the branched covering of the Teichmueller curve of the unfolded dodecahedron to the Teichmueller curve of the double pentagon. (Updated: December 19, 2019)
5. 3D_Figures.ipynb: This generates the code needed to run the 3D images of the dodecahedra on this webpage from the second paper. (Updated: May 1, 2020)

• Sage: Versions 8.9 and 9.0
• surface_dynamics: Version 0.4.0
• sage-flatsurf: Version 0.2

Acknowledgements

Updated: January 3, 2021