THE MOLECULAR DYNAMICS SIMULATION OF INTERACTIONS IN SHOCK-COMPRESED SYSTEMS

THE MOLECULAR DYNAMICS SIMULATION OF INTERACTIONS IN SHOCK-COMPRESSED SYSTEMS

V.S. Znamenski
Kabardino-Balkarian State University
P.O.Box 90, Nalchik-04, KBR
360004, Russia

P.F. Zilberman and I.N. Pavlenko
Kabardino-Balkarian State Agriculture Academy Nalchik, KBR, 360004, Russia

A general study of some atomic aspects of the shock and unload phenomena is presented. Computer molecular-dynamics simulations based on the Born-Maier-Huggins' and Poling's potential models has been used to study the shock-compression phenomena.

Introduction

This work is an extending development of our investigations on molecular dynamics simulation of contact melting [ 1-12] . Contact melting is a phenomenon of lowering of melting point at the contiguity zone of the two different crystals. Our molecular dynamics simulations showed that system of two contact bodies has the new physical properties. It happens when only masses and sizes of particles are difference in the difference sides of the boundary. And we are interest by the question: What will as a result of differences of other system parameters, as desksides of location of particles, group average velocities, and so on, on sides of section border of two materials forming the contact? Thus we started the studies of shock compressed systems [13] .

The research on shock - compressed conditions is closely connected with a work on production of amorphous materials, welding by explosion, making the artificial diamonds, and with other similar works. Molecular dynamics simulations has been broadly used to study microscopic features of substances. From the simulation, the time dependence of positions and velocities of particles are obtained by numerical integrating the equation of motion. Therefore, the MD method has been used to simulate a nonequilibrium phenomena. The MD method has been used to simulate crystallisation, glass formation [14] and melting processes for many system [15-16] .

Our studies were conduct for the ionic system. The alkali halides have been the preferred model system. Their physical and chemical properties have been widely investigated, and are well understood. There is a considerable interest in the understanding of phenomena by extreme conditions, for example, pressure-induced solid-solid phase transition [17] .

Some shock compression physical phenomena

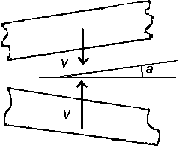
The feature of processes, which take place by the shock compression, is a structural modification of surface layers with practically absent of diffusion. In the Fig.1-2 you can see some simplified scheme of receiving of two aspects of shock compression phenomena. The welding by explosion is shown in Fig. 1 . The cumulative effect is shown in Fig. 2 . Beginnings of these processes are alike. Initial location and velocity of surfaces are shown in Fig 3 . The some combinations of the velocity V and the angle a are lead to a welding or a cumulation. The cumulative effect occurs when surfaces have the specific angle. Shock - compression conditions in the region of the collision of two surfaces gives these effects. It is known, that welding by explosion can connect two substances, which can not be connected by another ways. Importance technical significance has phenomenon of strengthening by explosion showed in Fig 4 .

MD simulation of the cumulative effect

The use of simulation on atomic scale is the possibly best means to finding - out for formation mechanisms under actions of shock loads and for revealing of processes, which take place thus. The molecular dynamic method (MD) allows to trace the movement of atoms or ions under the action of interparticle forces, and also to research the modification of its structures under actions of shock loads.

We made the simulation for ionic crystals with the BHM potential for various initial speeds. The estimate of structure characteristics was implemented by calculation of radial distribution functions (RDF) and by visualisation of particle trajectories. We note, that the RDF do not allows to find the great variety of structures, which are formed. Therefore it is possible to receive the maximal information only by visualisation of particle trajectories. We made the average of particle co-ordinates for the time of average in fluctuation period to the exception of influence of thermal fluctuations on visualisation. The MD-experiments had show the existence of strong processes of the structural rebuilding and the transfer to the amorphous structure under shock interaction in surface zone of several crystal layers. There are observed the cumulative effects on atomic scale of size. In Fig. 5 you can see the first simplified scheme of molecular dynamic experiment to study the shock - compression phenomena as the welding by explosion and the cumulative effect. The initial coordinates and velocities were randomly varied to provide the best fit to the expected effect.

Discussion

In our simulation we have recently discovered that sometimes certain ions move with more increased velocity and more linearly can be more long time. It happens by random configuration of particle. We would like to draw your attention to a question one can raise: Do observed properties really exist or they are only results of some calculation divergence? We specially examined situations, when calculation system has calculation divergence. It may by for example, when started position of two particles are at a very short, unrealistic distance. The system behaviour is absolutely different in this case. We think, that received property are true. We are study the problem.

We can say that there is same computer evidence for a commulation effect on the scale of hundred particles. With our small number of computer experiments, it does not seem reasonable to draw any definite conclusions as the mechanism of commutation. Our statistic are not rich enough to give conclusive results. Under the microscopic shock compression lattice becomes excited. We presuppose the stochastic shock influences are the ordinary events on normal conditions. The external shock action considerable increases the number of internal overshock events. These overshock have more stronger specific power. They are the basic reason such phenomena as welding by explosion and hardening be explosion. Atomic implication of this process is destruction of old structures and formation the new stable nodes. We should add, however, that MD simulation is very computer time consuming and our simulation result should be considered preliminary and our statistic are not rich enough to give the accurate confirmation of this our ideas.

MD simulation of substance properties in the shock- or unloading-wave

Different way to study the shock-compression is the simulation of a substance in (a) the significant increasing or (b) the decreasing of interatomic space. It is the simulation of substance properties (a) in the shock-wave or (b) in the unloading-wave. Modelling of shock compression was realised by the changing of the size of the calculation box. For simulation this effects we use same models. The first model started the calculation of the ion movements from nodes of the cubical net. Temperature has a broad range of values. First, we have constructed the initial coordinate and velocity of ions. Then by use of the numerical methods of temperature stabilisation we have make the run of MD simulations with different temperatures and values of size of cubic cell. One initial structure of particle system is regular cubic lattice of ions as for NaCl, and casual velocities. Second initial structure is some result of preceding MD simulations. The states of system have been examined by use of the mean square displacement R²_k(t) of ions

R²_k(t )= <r_i(t)-r_i(t_o)}²>_k (1)

where r_i(t) is position vector of i-th ion at time t, < > denoted the average, k denoted the type of ions.

We have developed a computer program, which can be used for simulation of many-bodies problem for classical systems with central interactions between particles, and can get an evolution in the time for ensemble of particles. The ensemble consists of 4 ion species, describing by the corresponding ion positions and velocities. The program allows one to get the mean-square displacements of ions, diffusion coefficients, partial radial distribution functions, normalised velocity autocorrelation functions and another data. Simulation was realised on traditional MD scheme with using the BHM [18] and Pauling's potentials. Number of all ions is 216, and the numbers of each type of ions are 64. Molecular Dynamics Simulation 54 A⁺ , 54 B^-, 54 C⁺, and 54 D^- were placed in the periodic cube. Our cubic simulation cell is divided initially by two equal parts corresponding to the AB and CD species respectively. The time step was 7-10 fs. At the initial stage of the MD simulation, NTV ensemble was settled. The data analyses were done with the final 1000 steps. The general statements of numerical experiments are given in table 1. The AB-CD notation denotes the following: chemical system AB is initially located in the first half of cubic cell and system BC is initially located in the second half. The A⁺,B^-,C⁺ ,D^-compound denotes an homogeneous ion mixture.

TABLE 1. The general statements of numerical experiments

System composition	Initial configuration of ions	Some details or/and purpose of experiment
NaCl-KBr	regular ideal cubic lattice	an effect of the ion exchange: Cl^- and Br-
Na⁺,Br^-,K⁺,Cl^-	amorphous state
NaBr-KCl	regular ideal cubic lattice
NaBr-KCl	regular ideal cubic lattice	locations of Br^- and Cl^- are fixed
Na⁺,Br^-,K⁺,Cl^-	amorphous state	locations of Br^- and Cl^- are fixed

The diffusion coefficients D_k (k=1,2,3,4) have been estimated by using the evolution parameters of a system and have been calculated by means of the relation

<{r_i(t )-r_i(t_o)}²>_k = 6 D_k t+ C_k , t_o< t< t, (2)

The velocity autocorrelation function is defined as,

Z_k(t)=<V_i(0)V_i(t)>_k/ <V_i²>_k (3)

where V_i is the velocity of ions, and k is a number of the ion type.
We have used here two potential approximations by Pauling [7] and Fumi-Tosi. The Pauling's potential between ions labelled "i" and "j" is given by

V_ij (r)= e²/(4 p e ₀ r )(q_i q_j r^-1 + [(s_i +s_j )/r]^p/(p +1)

(4)

where s are parameters, p = 8 (the hardness parameter), e₀ is the electric constant, q · e are the ionic charges, e is the electron charge.

The Fumi-Tosi potential is of the form

V_ij(r)= Z_iZ_je²/(4 p e₀ r ) + (1+ Z_i/n_i + Z_j/n_j) b exp[( s_i+ s_j-r)/ r]-C_ij/r⁶-D_ij/r⁸ (5)

here Z is an ionic charge number, n the number of the electrons in an outer shell, b a repulsion parameter, s a value characteristic of an ion size and r a softness parameter.

Results

We run a number of experiments consecutively varying sizes of cell and temperature, calculating diffusion coefficients. Beginning of sharp increasing the diffusion coefficients identifies the melting point. Herewith sharp increasing the diffusion coefficients is observe simultaneously for all types of ions, the difference is conclude at values of diffusion coefficient only. On the fig. 6 two area of phase diagram "solid -liquid" well stand out. Comparison of received results for systems NaCl-KBr and NaBr-KCl has show that for these systems phase diagrams "solid-liquid" are alike. If different systems are constitute of alike ions, temperatures of transition "solid-liquid" are alike for these systems for given sizes of cells. However values of diffusion coefficients of ions are different in the fluid phase. For instance diffusion coefficients of sodion in NaCl-KBr are smaller than in NaBr-KCl. Reduction of rib length of calculate cube from 2700 prior to 2550 pm brings about the raising of a melting point from 800 prior to 1500 K for NaCl-KBr system. Changing a pressure from 0 prior to 5 GPa corresponds to such changing a melting point. Other result is observe for the unordered mixture. The Amorphous state of such system is unchangeable when changing a size of cell (for given time of the experiment). Comparison shows that for the amorphous system the diffusion coefficients are vastly more high when accounting cell has the small sizes (Fig.7 ). Diffusion coefficient values for amorphous and regular systems become to be alike when increasing the sizes of cell prior to such, which are characteristic of liquid state of originally regular system.

We looked for system factors act on the ions diffusion. For instance we stopped some ions, assigning to them very great masses, to estimate how act on the diffusion of one ions a moving other ions. When we had freeze of all negative ions, the positive ions noticeably did not change their own diffusion coefficient values. It was characteristic for all system states.

Analysis of radial distribution functions has shown the following: Increasing a temperature of experiment brings about reducing a nearest distance between ions, which is reached due to heat moving of the ions for the originally ranked system. Interesting dependency is got at variation of cell sizes. Increasing the sizes of cell first brings about the growing of this feature, then to its reduction. For instance the least Na - Br distance increases from 2.7 prior to 2.9 A but then again decreases prior to 2.7. Such behaviour is explained by phase transition "solid- liquid". In the solid phase an increasing of the average distance between ions is accompany by the increasing of the minimum attainable distance. In the liquid phase appears a free volume by the cell size increasing, but the nearest ions again have the more close minimum distance to one another. Other result is observed for the unordered mixture of ions, what simulate the amorphous state: The initial increasing of the minimum distance between ions then changes onto the constancy. Similar dependencies are received for positions of first maximums of radial distribution functions, characterising average distances between nearby ions.

We have shown that MD method gives some reasonably reliable way to determining the microscopic characteristics of material at the shock compression phenomena. The simulation has show that for the temperature of experiment (T= 700-1500 K), and for a time of the experiment (t=1 ps) originally crystalline structure can be changed and formed amorphous or liquid state. The changing of the temperature and the cell size is accompanied by the changing of the time of the system transition into the amorphous state. Crystalline lattice is more stable under sprain stresses at the wave of unload, spraining together with the system. The growing of free volumes quickly becomes as a main mechanism of expansion of amorphous structure.

Acknowledgements

This work has been supported by the Russian Foundation of Basic Research under Grant No. 95-01-01567. The financial support of the Scientific Affairs Division of NATO is gratefully acknowledged.