|
[home] [CV] [Articles] |
THE MOLECULAR DYNAMICS SIMULATION OF CONTACT MELTING:
|
V.S. Znamenski
Kabardino-Balkarian State University
P.O.Box 46, Nalchik-04, KBR
360004, Russia
P.F. Zilberman
and I.N. Pavlenko
Kabardino-Balkarian State Agriculture Academy Nalchik, KBR
360004, Russia
Abstract
The results of several molecular dynamics
simulations are reported where an NaCl crystal is in contact with a KBr
crystal. Molecular Dynamics (MD) computer simulations have been performed
for a system of 216 ions interacting by means of the Born-Maier-Huggins'
or Poling's inter-ionic interaction potentials under contact melting conditions
over some range of densities.
1. Introduction
The fusion of two solids in a zone of contact when the temperature is lower than the fusion points of each crystal is known as contact melting (CM) [1-3] . Contact melting is widely used in various engineering processes and in physical chemistry analysis. It is successfully used to produce permanent joints, construction materials, alloys and chemical compounds. Contact melting serves in constructing fusibility diagrams and in simplifying investigations of diffusion processes. In particular, it allows one to easily determine inter-diffusion and partial diffusion coefficients.
For some time the problem of contact melting research on a nanometer-size scale was interest to scientists are engaged in studying this phenomenon. The basic questions are: what is occurring in the contact region and how do ions or atoms move there? Understanding the atomic processes occurring at the interface of two solids brought together at high temperature, is central to many technological problems, including soldering, and coagulation. We have applied a method of numerical simulation to find the answers to these questions - a molecular dynamics method (MD). The computer simulation gave a series of unsurprising results, from a physics point of view. For example, there are temperatures of contact melting and movement trajectories of surface ions. Some of our results are clearly an advance, but on the other hand, we can also evaluate CM parameters from first principles, describing interactions of ions in the melt at the interface. Simulations can show which ions interact more strongly, which ions interact more weakly, what happens, if diverse crystals are in contact, which ions will strengthen the interaction, and which will ease interactions. These results can deduce understanding of the nature of this phenomenon and also pose many new questions, thus opening up a new subject for research - the nanophysics of contact melting. Some of these questions are:
2. Contact Melting Problem
We addressed the problem of the contact-melting phenomenon on the nanometer scale by an MD-method, and our software was constructed on that basis. In our case, the application of the general MD-method is decided by the following two aspects of the problem:
The first aspect includes the following points:
1. Division of a calculation cell in two halves, a simulation, and accounting for of any statistical characteristics of the system separately for the particles which were originally placed in the first and second halves, divided by a contact border;
2. Monitoring features of dynamics of particles, and stipulated availability of a contact border. Comparison of the characteristics of a system when a contact border exists and after its disappearance (owing to diffusion of hashing of particles);
3. Variation of the mutual disposition of crystal lattices until the different state exists from a contact border.
The second aspect includes the following problems:
1. Research of the initial contact melting stage;
2. Research of dependence of contact-melting parameters from the fundamental characteristics; for example, the binary potential of interparticle interactions, effective radius of ions, rigidity of the repulsing part of potentials.
Software was developed for realisation of an MD-method for contact melting of ionic crystals. Personal computers permit one to study temperature dependencies of the ionic crystal and melt characteristics in a boundary zone. Analysis has shown, that the MD-method permits one to evaluate the characteristics by use of a personal computer of an IBM PC AT 486 type with arithmetic coprocessor. The methods accuracy is increased with application of more high-speed computers by means of expansion of a calculation base for statistical processing.
In the program part we used the following model:
1. The initial location of particles in the calculation box is represented by a cubic lattice; 1-2 and 3-4 ions occupy opposite halves of the box so as to imitate the contact between two heterogeneous substances. Here 1,2,3,4 are the numbers of the ion types.
2. The simulation box is a cube of constant edge length.
3. Periodic boundary condition are used.
4. Constant-temperature conditions are maintained by multiplying velocities by a calculated scaling coefficient.
5. The forces of pair interactions are initially calculated, and tables of f /r are used in simulations. Here f is the force; r is the distance between the particles; and i=1,2,...,10 is the type number of an interacting ion PRDF. Our simulations involved a total of 10 types.
3. Molecular Dynamics Simulations
The MD simulations were performed using a simple molecular dynamics algorithm for the NVT-ensemble (at constant N, number of molecules; V, volume; and T, temperature). The system NaCl-KBr studied consisted of 216 ions in a cubic box with the NaCl in the left side and KBr in the right side. The length of the box was variable for different experiments. The temperatures for calculations were chosen over a wide range including the contact melting temperature. In previous works; the calculations were executed for ionic three-component systems with a common anion or cation: sodium chloride-potassium chloride, sodium chloride-rubidium chloride, sodium iodide-potassium iodide, sodium chloride-sodium iodide, potassium chloride-potassium iodide [3] .
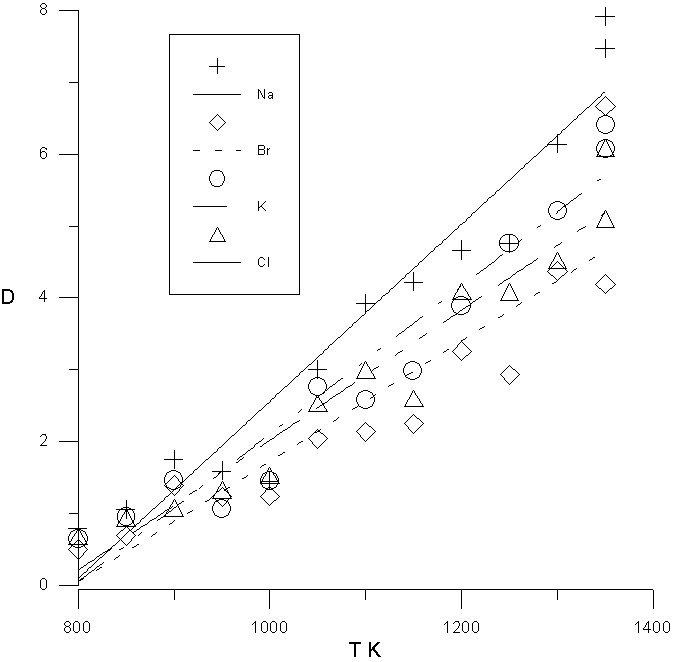
The mean-square displacements of ions were calculated in all numerical experiments and were hereinafter served for determination of the diffusion factors. It was found resulted that the diffusion coefficient of the sodion is more than the diffusion coefficient of the potassium ion and diffusion coefficient of the chlorion is more than the diffusion coefficient of the bromion. It is possible to explain this by the different size and mobility of these ions. It is shown, that the calculated diffusion factors are sensitive to the contact melting temperature and can be used for its valuation. The temperature dependence of the diffusion coefficients correspond to
D=A × exp(-E/RT).
In fig.1 the change in diffusion coefficients by contact melting temperatures is shown.
The calculated results were obtained using potential approximations for pair interactions based on simplified Poling's and Born-Maier-Huggins' potentials. The results are compared with experimental data [1-3] .
4. Partial Radial Distribution Functions
Partial radial distribution functions (PRDF) for different temperatures were also obtained. For the 900 K melt temperature, the parameters of PRDF ( location of first nonzero value, location of first maximum, values of first maximum) are presented in table 1.
Table 1. Parameters of PRDF
|
Na-Na |
Na-Br |
Br-Br |
Na-K |
Br-K |
K-K |
Na-Cl |
Br-Cl |
K-Cl |
Cl-Cl |
|
Loc. of first nonzeros, 10 -10 m |
3.30 |
2.78 |
4.14 |
3.72 |
2.99 |
3.93 |
2.67 |
4.03 |
2.99 |
3.82 |
|
Loc. of first maxima, 10 -10 m |
11.23 |
3.22 |
6.17 |
6.49 |
3.71 |
6.49 |
3.11 |
5.75 |
3.74 |
5.96 |
|
First maxima |
1.7 |
4.1 |
1.9 |
1.9 |
4.0 |
2.0 |
4.5 |
1.9 |
3.7 |
1.8 |
The location of the first nonzero value for ions of different types (anion-cation) is less then the location of the first nonzero value for ions of similar type (anion-anion, cation-cation). The values of the first maximum for ions of different types (anion-cation) is more, than the values of the first maximum for ions of similar types (anion-anion, cation-cation).
The values of the first maximum for ions of different types (anion-cation) for Na-Cl is more than for Na-Br, K-Br, K-Cl.
The values of the first maximum for ions of similar types (anion-anion, cation-cation) for K-K is more, than values of the first maximum for Na-K, Br-Cl, Br-Br, Na-Na.
The temperature dependencies obtained the PRDF parameters are used for the zone of contact. The increase of temperature is accompanied by a reduction in space to the first nonzero value of PRDF.
We shall note, that location accuracy of the maximum of the second co-ordination sphere is far below, in view of the difference of these maxima.
Modelling conducted for various temperatures specified a significant extension of maximas for the first and the second coordinate sphere. Intensity of these maximas was reduced. It is possible also to note, that the position of the first maximum in a crystal is higher than for melts, and with growth of temperature is observed an insignificant increase is observed.
The computer simulation of contact melting is one more check on adequacy of using pair interaction potentials. As was shown, we used simplified Poling's potential and a more complicated Born-Maier-Huggins' potential [4] . The first of them, for a NaCl-KBr system, has given results in better agreement with experiment.
5. Normalized Velocity Autocorrelation Functions
The normalized velocity autocorrelation functions are calculated for ionic systems in a boundary zone by a contact-melting mode. An oscillation part is typical for velocity autocorrelation functions of ionic systems, as well as for liquid metals. We used the following data as characteristic parameters for velocity autocorrelation functions: (1) first passage times of the first minimum; (2) value of the first minimum. For this system it was found: 1- Na 84 fs, Br 190 fs, K 135 fs, Cl 113 fs; 2 - Na 0.45, Br 0.30, K 0.43, Cl 0.45. Comparing molecular-dynamic experiments with one-component ionic systems by repeating some other known analyses, has shown consistency of our results with the results of other authors.
6. Conclusions
1. The initiation of contact-melting is characterised by increased mobility of ions, which is observed by extended trajectories of ions on the contact border;
2. The mobility of ions in contact depends on a mutual disposition of lattices;
3. The microscopic mechanism of contact melting includes a formation of liquid-phase clusters in micro-volumes (size of the order 2 nm; for time scales it is of the order of program facilities). Cluster behaviour is unstable, but it can initiate the beginning of a liquid phase.
4. The beginning of contact melting is
characterised in the contact zone by increasing distance between the nearest
anion and cation, and the intensity of interaction grows, for those anion-cation
pairs, which have in a similar system, higher intensity of interaction;
for other pairs, the intensity decreases
7. Acknowledgements
This work has been supported by the Russian Foundation of Basic Research under Grant No. 95-01-01567. The financial support of the Scientific Affairs Division of NATO is gratefully acknowledged.
8. References
D x 10 5 , cm 2 /s

Figure 1 . The temperature dependence of the diffusion coefficient D x 10 5 , cm 2 /s. for Na + , Br - , K + , Cl - .