BEHAVIORAL ADAPTATION
DINOSAUR RUNNING SPEED
Many dinosaurs, probably most, had lifestyles or preferred habitats that brought them into contact with the shorelines of lakes, rivers or ocean. Some may have spent all their lives in such locales, while others may have only gone there occasionally to drink, find food, mate, or satisfy other life necessities. Some may simply have crossed bodies of water when migrating to a distant home range. For whatever reason they were there, these dinosaurs, like animals in such places today, left their footprints in the soft sand and mud of the beaches, banks and bars of the shoreline environments through which they traveled. Most of these footprints were undoubtedly quickly eradicated by shifting winds, tides, or sands. But many were not. Rapid burial of some prints by new layers of sediment protected them from later obliteration, and when these sediments were lithified, the footprints were preserved as impressions in the hard rock.
1. STATEMENT OF PROBLEM: Analysis of dinosaur footprints and trackways (a series of footprints made by an animal as it moves forward) is a powerful tool in understanding important aspects of dinosaur behavior. For example, analysis of trackways in Cretaceous limestones of central Texas indicates that some sauropod dinosaurs (e.g. “brontosaurs”) traveled in herds, with the smaller juveniles in the center of the herd, and the larger adults posted on the periphery, presumably for protection of the young. This lab exercise illustrates how one can determine from trackways how fast one dinosaur was traveling.

2. METHOD OF ANALYSIS: The approach we will take to resolve the question of dinosaur running speed is to analyze the size and spacing of dinosaur footprints, and to compare the results to data for living animals, whose running speeds we can observe and measure directly. The underlying premise is that as an animal runs faster, its legs swing in a wider arc, and its footprints will become more widely spaced. Footprint spacing thus increases with speed. If you think about how you walk and run, this relation between speed and stride, should become immediately obvious. For this reason, and because humans and the dinosaur in question are both bipedal (move on two legs), we can use humans as a modern analog for dinosaurs.
We will also have to concern ourselves with the fact that many dinosaurs are larger than most modern animals, including humans. We will, therefore, need a way to scale speed/size data for humans up to the size of dinosaurs. If we can find a scaling rule for doing this, then we can estimate dinosaur running speed from footprints preserved in rock.
In detail, our methodology will be:
A. Define & measure footprint and trackway parameters
B. Define & measure body dimensions useful in calculating running speed
C. Determine scaling rule relating running speed and body size
D. Determine human running speed experimentally
E. Calculate human & dinosaur running speed from trackway metrics & scaling rule
F. Evaluate accuracy of trackway analysis by comparing calculated and experimental measurements of human running speed
You will find it helpful to work in groups to collect the data needed to complete this lab. One convenient way to do this is for everyone at a given lab bench to work together on this problem. Ideally, a research group will consist of 4 or 5 people. Data for the group should be pooled and used by everyone in the group.
3. NECESSARY EQUIPMENT, SUPPLIES, & SPECIMENS: To determine dinosaur running speed, we require the following:
A. dinosaur trackway
B. human “guinea pig”
C. meter sticks for measuring trackway & body dimensions
D. tape measure for laying out speed test track
E. stopwatches for timing human runner
F. chalk or marker poles for demarcating speed test track
4. DINOSAUR TRACKWAY: Because trackways of dinosaurs generally can not be cut out of the rock into which they are inscribed without destroying them, we will take another approach. We will use the dinosaur “trackway” painted on the floor of the hallway outside the lab. This corridor trackway was made by placing cardboard sheets on top of real dinosaur tracks preserved in sandstones originally comprising the soft, wet shoreline sands of an ancient lake. The outline of a footprint was traced onto the cardboard, and the cardboard was then cut into the shape of the footprint. The cut-outs were used as templates to paint the trackway on the floor. The trackway reproduced in the hallway faithfully duplicates not only the shape and size of the footprints, but also their relative positions in the trackway. Thus, it records the actual steps made by an individual dinosaur as it moved across a mudflat at the edge of this ancient lake.
The trackway we will use was made by Dilophosaurus, a carnivorous dinosaur of the late Triassic (185 my {million years ago}). The original prints were found in Ryker Hill Park , Roseland , NJ . In appearance, Dilophosaurus resembles the more widely known Tyrannosaurus of the late Cretaceous (70 my). Figure 3.6 diagrams the appearance of a typical dilophosaur. The animal that made our tracks was an adult approximately 20 feet long and weighing about 1000 pounds.We want to find the speed of our dilophosaur from the size and spacing of its footprints. To do this, you will need to keep in mind the posture of Dilophosaurus (see Figure 3.6), and distinguish between its left and right feet.

FIGURE 3.6: Sketch of Dilophosaurus chasing turtles

Dilophosaurus, like all carnivorous dinosaurs, had a bipedal posture, and thus walked on its back legs only. The front legs (arms and hands really) were used for grasping, not for walking (it is interesting to note that carnivorous dinosaurs, and humans and other primates, are the only animals to have evolved grasping hands). Notice that the body was held horizontally with the tail extending backwards to balance the weight of the body over the hips. Bipedal dinosaurs did not stand erect as bipedal humans do. The trackway reproduced in the corridor represents a sequence of left/right footfalls or steps made as the animal moved forward. Notice also that an individual footprint shows the impressions of only three toes. This is because carnivorous dinosaurs had bird-like three toed feet (like chickens and pheasants, carnivorous dinosaurs had a small backward pointing fourth toe, but this toe did not reach the ground, and left no indication of its presence in footprints).

FIGURE 3.6: Sketch of Dilophosaurus.

1. DEFINITION OF LOCOMOTOR PARAMETERS: To estimate running speed from the trackway, you will need to determine several important dimensions of the dilophosaur's body. The dimensions of interest include body parts (e.g., legs, feet) that are directly involved in locomotion. You will need to determine the same body dimensions for humans also. In particular, you will need to know: 1) foot length; 2) hip height (= leg length); and 3) stride length. These parameters are defined in Table 1, and in Figure 3.7. The data for humans will be used to check the accuracy of the method for calculating running speed in dinosaurs.
TABLE 1: Definition of dinosaur and human locomotor parameters
PARAMETER
|
SYMBOL
|
DEFINITION |
Foot Length |
F |
Length of foot from tip of longest digit to heel.
Measured as greatest front-to-back distance of a footprint.
|
Hip Height
|
H
|
Height of the hip joint above the ground. Hip height is equivalent to leg length, and is measured as the distance between the ground and the ball-and-socket joint of the hip.
|
Stride Length
|
S |
Distance between successive footfalls of the same foot. Stride length must not be confused with pace length which is the distance of a single step, i.e. the distance between footfalls of the left and right foot. Stride length generally equals twice the pace length.
|

FIGURE 3.7: Definition of dinosaur locomotion parameters.
Hip height (H) can not be measured directly for our dilophosaur because the animal making the trackway was not preserved along with its tracks. But we can use equation 1, to estimate hip height from foot length (F):
Equation 1: H = 5 * F.
This relation has been verified for a variety of dinosaurs and modern vertebrates also. The equation states simply that hip height (or leg length) is about 5 times foot length in vertebrates (including dinosaurs) that walk and run on two legs.
6. MEASUREMENT OF LOCOMOTOR PARAMETERS: Each research group has two tasks that must be performed in order to successfully evaluate running speed in dinosaurs:
1) measure the locomotor parameters for Dilophosaurus from the footprints on the corridor floor.
2) determine human speed by measuring locomotor parameters and running speed for ONE member of the group.
Only one member of each group should be selected by the group as the “lab specimen” for this test. This will simplify the testing procedure, but will still give reliable results. The person selected must be wearing sneakers or rubber soled shoes. This will insure that the testing proceeds with a minimum likelihood of slipping or falling.
6.1 Dilophosaurus Locomotor Parameters: Measure foot length (F) and stride length (S) for Dilophosaurus from the “trackway” in the hallway using the tape measure provided. Record the results in the appropriate spaces in Table 2, below. Calculate hip height (H) using equation 1, and record this information in Table 2 also. Be sure to make all your measurements in the metric system. If you used the English system convert from feet to meters by using the conversion factor of 1 ft = 0.3 m.
TABLE 2: Locomotor data for dinosaurs and humans. Measured H – hip height as determined from measurement. Calculated H – hip height as calculated from foot length. N/A indicates measurements that cannot be made.
SPECIMEN
|
FOOT
LENGTH
(F) |
HIP HEIGHT
(H) |
STRIDE
LENGTH
(S) |
Measured H |
Calculated H
|
Dilophosaurus |
|
N/A |
|
|
|
|
|
|
|
6.2 Human Locomotor Parameters: Each research group should now repeat the process for finding the parameters in Table 2, but this time determine F, S, and H for the group's runner, and enter the data in the appropriate spaces in Table 2. First, however, enter the runner's name in the “Specimen” column of Table 2, in the space beneath that for the dinosaur. Do the same in Table 4 and Table 6.

Foot Length: Measure the foot length of your research group's runner from toe to heel. Record the data in the appropriate place in Table 2.
Hip Height: To measure hip height, your group's runner should stand erect, and with the tape measure, a second member of the group should determine the distance between the floor and the runner's hipbone (i.e., the widest part of his/her hips). The result is the runner's hip height. Enter this distance in the appropriate place in Table 2.
Stride Length: To find your runner's stride length, it will be necessary for him/her to run the length of a measured course laid on the College Quadrangle. The procedure for measuring stride length consists of the steps outlined below. Make sure that you perform each one correctly, and in the proper sequence. Once again be sure all your measurements are in the metric system.
A. The distance across the College Quadrangle, from the concrete sidewalk in front of Ingersoll Hall to the concrete sidewalk in front of Boylan Hall, is exactly 50 m, as diagrammed in Figure 3.7a.
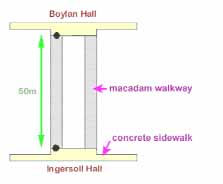
FIGURE 3.7a: Quadrangle race course
B. One student should now be designated as the group's “counter”, and the other two or three as “timers”. The job of the counter is to count the number of stride's made by the group's runner as he/she proceeds down the measured course. The job of the timers is to measure, using the stopwatches, the time required for the runner to travel the length of the course. The timers should practice with the stopwatches to make sure they understand how to use them before the test is actually made.
C. When all is in readiness, the runner should step up to the starting line. The timers should be ready to start their instruments. The counter gives the “GO” signal, whereupon the runner runs to the end of the course. The counter counts the total number of strides made by the runner in running the course; and the timers measure the time needed for the runner to reach the finish line. Stride and timing data should be entered in the appropriate places in Table 3.
CAUTIONARY NOTE TO RUNNER: It is not necessary to run as fast as possible to make this study successful. A half speed or three quarter speed run is advised.
TABLE 3: Raw data for human speed trial
Length of
Test Course |
Number of
Strides |
Time
(Timer #1) |
Time
(Timer #2) |
Time
(Timer #3) |
|
|
|
|
|
It is now a straightforward task to obtain the runner's stride length (S) from the following relation:
Equation 2: S = (distance run)/number of strides).
Record your runner's stride length in the appropriate space in Table 2.
7. DILOPHOSAUR RUNNING SPEED: We now have all the data needed to calculate running speed from foot length and stride length for the dilophosaur. However, we still need a way to account for the difference in size between Dilophosaurus and humans. One way to do this is to resort to an empirical relation of size and speed, derived from speed trials done on a diverse array of living animals. If the animals tested cover a wide size range, from mice to elephants for example, the resulting data set would incorporate data from animals both larger and smaller than humans and dilophosaurs. In this way, it should be possible to address the issue of size dichotomies between humans and our dilophosaur, and the effects of such on speed. Such data are plotted in Figure 3.8, on the next page.
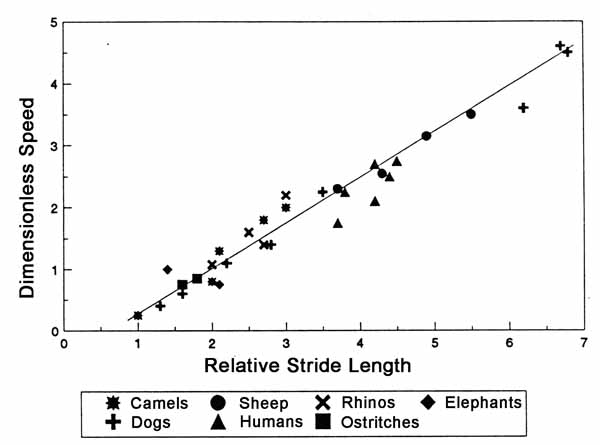
Figure 3.8: Size independent performance for animals listed in the legend. Relative stride length and dimensionless speed are defined in the text below.
We see in Figure 3.8, that the size/speed data plot very clearly along a straight line. The straight line thus defines the relationship between speed and size. Since the data include animals widely disparate in size, posture (some are bipedal, some quadripedal), and systematic status (birds and mammals), the relationship expressed by this line is probably a very robust one, and thus one we can feel confident about it in terms of estimating dilophosaur running speed.
There is a problem with Figure 3.8, however, and that is that the parameters shown on the X and Y axes of the graph are not ones we have yet dealt with. What, for example, is relative stride length, and what does “dimensionless speed” mean? These uncertainties need to be cleared up before we can finalize our results with regard to dilophosaur speed.
In essences, by using the parameters in Figure 3.8 rather than using simple size or speed, we can factor out the effect of size. Thus, we define relative speed as:
Relative Stride Length = (Stride Length)/(Hip Height) = S/H. Eq. 2
and
Dimensionless Speed = (Actual Speed)/(10 · Hip Height) 1/2
Eq. 3
Note that the denominator of this equation 3, involves a simple exponentiation, that is, you need to find the square root of 10 times hip height. Defining denominator in this way allows us to account for the influence of gravity which acts when an animal swings its leg forward when it moves. It is also crucial to stress that these equations only work, if you are using the metric system for your measurements (this is because 10 is the gravitational constant in the meter-kilogram-second system). If you are using anything except meters for distance, and meters/sec for speed, you will get incorrect results from these equations.
Calculate the relative stride length and dimensionless speed of your human runner from eqations 2 and 3 on the revious page, and indicate his/her position in the plot in Figure 3.8 with a symbol different than used for the other animals plotted in this figure.
1. Is the performance of your human runner comparable to that of the animals, including other humans, included in Figure 3.8?
Yes ______________ No ______________
Explain:
Now we can find the actual speed of the dilophosaur that made the corridor trackway. This may be done by calculating the relative stride length of the dilophosaur using equation 2, and then using Figure 3.8, and equation 3 to find its actual speed.
What is the dilophosaur's relative stride length ________________________
What is the dilophosaur's dimensionless speed ________________________
What is the dilophosaur's actual speed ________________________
CONCLUSIONS: What do the speed results for Dilophosaurus indicate about the concept that dinosaurs were slow, plodding creatures?
What do the results indicate about your chances of escaping from a hungry dilophosaur if you were to meet one?
POST-SCRIPT. Consider that a well-trained human athlete, capable of running a 4 minute mile is moving at only 15 mph, i.e., at a speed less than for our dilophosaur. Also, consider that we can't be sure that the dilophosaur was running at its top speed. Perhaps it could run even faster. After all, animals rarely can travel at their fastest when traversing the kind of soft, sticky river bank mud this dinosaur was trying to negotiate when it made these footprints (Can you run at your top speed on a beach?)
We see in this dichotomy in performance between dinosaurs and humans one reason why dinosaurs dominated terrestrial ecosystems during the Mesozoic Era, and why during these times, life was hard for small, defenseless mammals. It is perhaps somewhat comforting to know that dilophosaurs and humans never met. Dinosaurs became extinct more than 60 million years before the earliest human ( Homo ergaster ) appeared in central Africa .

Click here to go back to go back to the main page
Department of Geology
Brooklyn College
Brooklyn, NY 11210










